Some interesting sorting algorithms

Walking back from Falafels today with CS majors, we somehow began discussing strange sorting algorithms.

A good sort to know (not really) is bead sort. Imagine you have a bunch of beads on rods, like an abacus, and cross-wise they represent numbers. If you simply tilt the whole thing over, then gravity will let them all fall and they’ll sort themselves. For example, we have the numbers 3, 2, 4, and 2 read horizontally. When they fall, we get 2, 2, 3, 4. Easy!

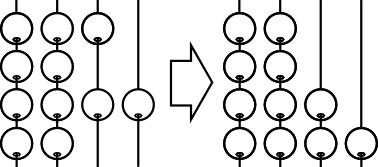
Another sort, “random sort,” “shuffle sort,” or the more common name “bogosort” was suggested as a good example of an O(?) algorithm. But, as people have pointed out, if the quantum many-worlds theory holds, then you could sort in O(n) time: Use true quantum randomness to randomize the list and if the list is not sorted, then destroy the universe. The only universe that remains will have a sorted list.

Finally, Graham showed me the wonders of sleep sort. I’ll just leave the bash source code here:

[bash]
seq="1 9 2 3 5 6 4 7"
for i in $seq; do
(sleep $i;echo $i)&false;
done
[/bash]